快速排序

package com.weidd.best.sort;

/**
 * @program: SortDemo
 * @author: weidd
 * @date: 2020-12-07 20:53
 * 快速排序：  QuickSort 思想：分治
 * 指针交换法、挖坑法
 * <p>
 * 1：从数组中找出一个元素作为基准（pivot）。
 * 2：排序，将所有比基准数小的放到基准的左侧，比基准大的放到基准的右侧。该操作称为分区（partition）
 * 3：递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；
 * <p>
 * 指针交换：
 * 1：
 **/
public class QuickSort {
    public static void main(String[] args) {
        int[] arr = {1, 34, 88, 5, 6, 7, 3, 7, 66};
        long start = System.currentTimeMillis();
        sort(arr, 0, arr.length - 1);
        System.out.println(System.currentTimeMillis() - start);
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ,");
        }

    }

    private static void sort(int[] arr, int left, int right) {

        if (left >= right)//递归的结束条件，非常重要
            return;

        //重要是先获取基准对应下标，在获取基准下标的过程中将数组分成两个分区
        int pivotIndex = getPivotIndex(arr, left, right);
        // 然后再用递归，排出左右分区。
        sort(arr, left, pivotIndex - 1);
        sort(arr, pivotIndex + 1, right);
    }

    //获取基准值对应数组下标
    private static int getPivotIndex(int[] arr, int left, int right) {
        // 定义一组变量，i,j为左右指针，temp为左右交换时的临时变量，pivot为基准值。
        int i, j, temp, pivot;
        i = left;
        j = right;
        pivot = arr[left];

        while (i != j) {
            while (pivot <= arr[j] && j > i)
                j--;
            while (pivot >= arr[i] && j > i)
                i++;
            // 交换左右指针对应的值
            if (j > i) {
                temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        arr[left] = arr[i];
        arr[i] = pivot;
        return i;
    }
}

import org.junit.Test;

/**
 * @program: SortDemo
 * @author: weidd
 * @date: 2020-12-08 12:09
 **/
public class Test01 {
    @Test
    public void test1() {
        int[] arr = {3, 5, 8, 2, 1, 9, 0, 6, 7, 4};
        quickSort(arr, 0, arr.length - 1);
        for (int i = 0; i < arr.length; i++) {
            System.out.print(i+" ,");
        }
    }

    private void quickSort(int[] arr, int left, int right) {
        if (left > right)// 此为递归的结束条件，
            return;
        int middle = getMiddle(arr, left, right);// 此步最为关键
        quickSort(arr, 0, middle - 1);
        quickSort(arr, middle + 1, right);

    }

    private int getMiddle(int[] arr, int left, int right) {
        int temp = arr[left];
        while (left != right) {
            // 右指针左移
            while (right > left && arr[right] >= temp)
                right--;
            // 左指针右移
            arr[left] = arr[right];// 先将右边给左边
            while (right > left && arr[left] <= temp)
                left++;
            arr[right] = arr[left]; // 将左边给右边。
        }
        arr[left] = temp;
        return left;
    }
}

原理:

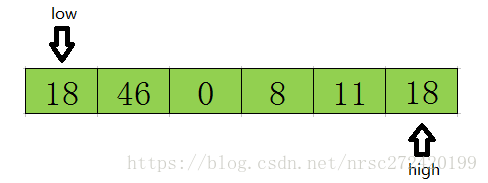
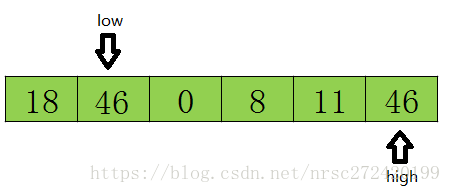
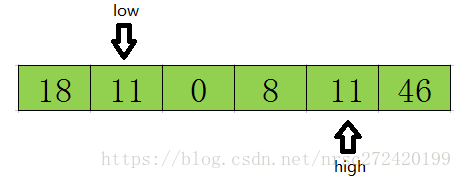
   快速排序,说白了就是给基准数据找其正确索引位置的过程.    如下图所示,假设最开始的基准数据为数组第一个元素23,则首先用一个临时变量去存储基准数据,即tmp=23;然后分别从数组的两端扫描数组，设两个指示标志:low指向起始位置，high指向末尾.    首先从后半部分开始，如果扫描到的值大于基准数据就让high减1,如果发现有元素比该基准数据的值小(如上图中18<=tmp)，就将high位置的值赋值给low位置 ,结果如下: 然后开始从前往后扫描,如果扫描到的值小于基准数据就让low加1,如果发现有元素大于基准数据的值(如上图46=>tmp)，就再将low位置的值赋值给high位置的值,指针移动并且数据交换后的结果如下: 然后再开始从后向前扫描,原理同上,发现上图11<=tmp,则将low位置的值赋值给high位置的值 ,结果如下: 然后再开始从后向前扫描,原理同上,发现上图11<=tmp,则将high位置的值赋值给low位置的值,结果如下: 然后再开始从前往后遍历,直到low=high结束循环,此时low或high的下标就是基准数据23在该数组中的正确索引位置.如下图所示.   这样一遍走下来,可以很清楚的知道,其实快速排序的本质就是把基准数大的都放在基准数的右边,把比基准数小的放在基准数的左边,这样就找到了该数据在数组中的正确位置.   以后采用递归的方式分别对前半部分和后半部分排序，当前半部分和后半部分均有序时该数组就自然有序了。

一些小结论

从上面的过程中可以看到:

  ①先从队尾开始向前扫描且当low < high时,如果a[high] > tmp,则high–,但如果a[high] < tmp,则将high的值赋值给low,即arr[low] = a[high],同时要转换数组扫描的方式,即需要从队首开始向队尾进行扫描了   ②同理,当从队首开始向队尾进行扫描时,如果a[low] < tmp,则low++,但如果a[low] > tmp了,则就需要将low位置的值赋值给high位置,即arr[low] = arr[high],同时将数组扫描方式换为由队尾向队首进行扫描.   ③不断重复①和②,知道low>=high时(其实是low=high),low或high的位置就是该基准数据在数组中的正确索引位置.

按照上诉理论我写的代码如下:

package com.nrsc.sort;

public class QuickSort {
    public static void main(String[] args) {
        int[] arr = { 49, 38, 65, 97, 23, 22, 76, 1, 5, 8, 2, 0, -1, 22 };
        quickSort(arr, 0, arr.length - 1);
        System.out.println("排序后:");
        for (int i : arr) {
            System.out.println(i);
        }
    }

    private static void quickSort(int[] arr, int low, int high) {

        if (low < high) {
            // 找寻基准数据的正确索引
            int index = getIndex(arr, low, high);

            // 进行迭代对index之前和之后的数组进行相同的操作使整个数组变成有序
            //quickSort(arr, 0, index - 1); 之前的版本，这种姿势有很大的性能问题，谢谢大家的建议
            quickSort(arr, low, index - 1);
            quickSort(arr, index + 1, high);
        }

    }

    private static int getIndex(int[] arr, int low, int high) {
        // 基准数据
        int tmp = arr[low];
        while (low < high) {
            // 当队尾的元素大于等于基准数据时,向前挪动high指针
            while (low < high && arr[high] >= tmp) {
                high--;
            }
            // 如果队尾元素小于tmp了,需要将其赋值给low
            arr[low] = arr[high];
            // 当队首元素小于等于tmp时,向前挪动low指针
            while (low < high && arr[low] <= tmp) {
                low++;
            }
            // 当队首元素大于tmp时,需要将其赋值给high
            arr[high] = arr[low];

        }
        // 跳出循环时low和high相等,此时的low或high就是tmp的正确索引位置
        // 由原理部分可以很清楚的知道low位置的值并不是tmp,所以需要将tmp赋值给arr[low]
        arr[low] = tmp;
        return low; // 返回tmp的正确位置
    }
}

package com.weidd.best.dataStructureandAlgorithms.algorithms.sort;

/**
 * @program: SortDemo
 * @author: weidd
 * @date: 2020-12-19 18:28
 **/
public class QuickSort1 {

    public static void main(String[] args) {
        int[] arr = {1, 3, 2, 5, 7, 2, 4};
        quickSort(arr, 0, arr.length - 1);
        for (int i = 0; i < arr.length; i++) {
            System.out.print(i + " ,");
        }
    }

    private static void quickSort(int[] arr, int left, int right) {

        if (left >= right)// 递归的结束条件，重要。
            return;
        // 重要操作：获取基准值对应的数组下标，此过程完成以基准为分界的左右分区。
        int middleIndex = getMiddleIndex(arr, left, right);
        quickSort(arr, left, middleIndex - 1);
        quickSort(arr, middleIndex + 1, right);
    }

    private static int getMiddleIndex(int[] arr, int left, int right) {
        //以数组起始位置值作为基准值。
        int temp = arr[left];
        while (left != right) {

            while (right > left && arr[right] >= temp)
                right--;
            arr[left] = arr[right];
            while (right > left && arr[left] <= temp)
                left++;
            arr[right] = arr[left];
        }
        arr[left] = temp;
        return left;
    }
}