算法题:
- 数据结构:数组、链表、字符串、树、数学、栈、hash表、图
- 动态规划、中心扩散、回溯算法、递归、迭代、贪心算法、
- 从整体到细节,自顶向下,从抽象到具体的框架思维是通用的,不只是学习数据结构和算法,学习其他任何知识都是高效的。
一、数组:
技巧:
- 双指针
11. 盛最多水的容器
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
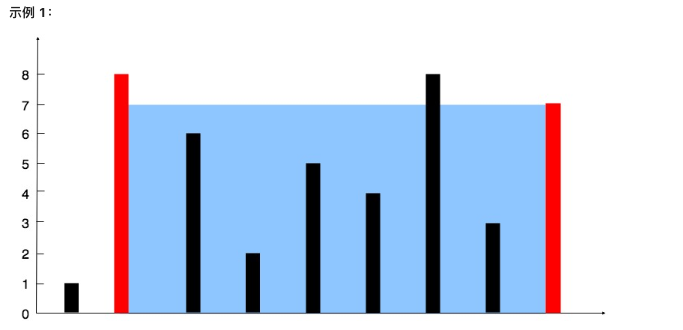
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
class Solution {
public int maxArea(int[] height) {
//木桶原理:盛放最多水的量是根据木桶的最低木块决定的。
// 双指针:(左指针指向数组索引最小值,右指针指向数组索引最大值。通过移动左右指针找到【数组索引差*对应索引对应的最小值】) 判断盛放最大量水,要根据两个索引对应的值的最小。
//双指针:快慢指针,左右指针。
int l=0 , r =height.length-1;
int ans=0;
while(l!=r){
if(height[l]>height[r]){
ans=Math.max(ans, (r-l)*height[r]);
r--;
}else{
ans=Math.max(ans, (r-l)*height[l]);
l++;
}
}
return ans;
}
}
15. 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = [] 输出:[] 示例 3:输入:nums = [0] 输出:[]
算法流程:
- 特判,对于数组长度 n,如果数组为 null 或者数组长度小于 3,返回 []。
- 对数组进行排序。
- 遍历排序后数组:
- 若
nums[i]>0:因为已经排序好,所以后面不可能有三个数加和等于 0,直接返回结果。 - 对于重复元素:跳过,避免出现重复解
- 令左指针 L=i+1,右指针 R=n-1,当L<R 时,执行循环:
- 当 nums[i]+nums[L]+nums[R]==0,执行循环,判断左界和右界是否和下一位置重复,去除重复解。并同时将L,R移到下一位置,寻找新的解
- 若和大于 0,说明nums[R] 太大,R左移
- 若和小于 0,说明 nums[L] 太小,L 右移
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
//先排序,再定义三个指针,遍历数组,nums[i]=nums[j]+nums[k];将三个值问题转成求两个和等于第三个问题。
List<List<Integer>> listT = new ArrayList<List<Integer>>();
//base case
if(null==nums||nums.length < 3) return listT;
//对数组进行排序(重要的一步)
Arrays.sort(nums);
for(int i=0;i<nums.length;i++){
if(nums[0]> 0) break;//最小的数大于0 .所有的值都大于零。直接结束
int j =i+1, k=nums.length-1;
//去重
if(i>0 && nums[i]==nums[i-1]) continue; //去重
while(j<k){
int temp =nums[i]+nums[j]+nums[k];
if(temp==0){
listT.add(Arrays.asList(nums[i],nums[j],nums[k]));
while(j<k &&nums[j]==nums[j+1] ) j++; //去重
while(j<k &&nums[k]==nums[k-1] ) k--; //去重
j++;
k--;
} else if (temp>0){
k--;
}else{
j++;
}
}
}
return listT;
}
}
53. 最大子序和
给定一个整数数组
nums,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。 示例 2:
输入:nums = [1] 输出:1 示例 3:
输入:nums = [0] 输出:0 示例 4:
输入:nums = [-1] 输出:-1 示例 5:
输入:nums = [-100000] 输出:-100000
class Solution {
public int maxSubArray(int[] nums) {
// 动态规划做题
// 初始化两个值: 当前值的和, 最大值
// 此题的关键点在于: 当前和a + 当前值b = c ,与当前值b的比较,c>b 返回,c ;否则返回b,b作为加上当前值的和
//最后一步比较加上当前值b后的和,与最大值做比较。返回和的最大值。
int pre = 0, maxValue=nums[0];
if(nums.length==1) return nums[0];
for(int x : nums){
pre =Math.max(pre+x,x);
maxValue=Math.max(pre,maxValue);
}
return maxValue;
}
}
121. 买卖股票的最佳时机 (动态规划问题)
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4] 输出:5 解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
class Solution {
public int maxProfit(int[] prices) {
//双重循环能求出: 此方法会报超出时间限制,不能用。
/*int len =prices.length;
int max =0;
for(int i=0;i<len;i++){
int pre =0;
for(int j=i+1;j<len;j++){
max =Math.max(max, prices[j]-prices[i]);
}
}
return max;*/
//方式2: 使用动态规划来解此题。
int min =prices[0],max =0;
for(int i =1;i<prices.length;i++){
max=Math.max(max,prices[i]-min);
min=Math.min(min,prices[i]);
}
return max;
}
}
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12] 输出: [1,3,12,0,0]
说明:
- 必须在原数组上操作,不能拷贝额外的数组。
- 尽量减少操作次数。
class Solution {
public void moveZeroes(int[] nums) {
// 双指针法(方式一:将非0数往左移,最后补零)
/*int i=0 , j =0, n=nums.length;
while(j < n){
if(nums[j]!=0){
nums[i++]=nums[j];
}
j++;
}
while(n-i>0){
nums[i++]=0;
}*/
// 双指针法(方式二:左右指针,发现右指针不为0,就将左右互换位置,遍历结束。0都在右侧)
int r = 0, l = 0, n = nums.length;
while(r<n){
if(nums[r]!=0){
swap(nums,l,r);
l++;
}
r++;
}
}
void swap(int[] nums, int l,int r){
int temp =nums[r];
nums[r]=nums[l];
nums[l]=temp;
}
}
二、链表:
技巧:
- 链表问题一般先定义一个哑结点,将特殊清除处理掉
链表反转
private Node reverse(Node node) {
Node pre = null, cur = node, tem = null;
while (cur != null) {
tem = cur.next;
cur.next = pre;
pre = cur;
cur = tem;
}
return pre;
}
2. 两数相加
难度中等 6174
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
// 特判:
if(l1==null)return l2;
if(l2==null)return l1;
int carry=0;
ListNode dummy =new ListNode(0);// 定义个哑结点,便于处理
ListNode pre=dummy; // 指向哑结点的地址、最终返回pre.next;
while(l1!=null && l2!=null){
int sum =l1.val+l2.val+carry;
carry =sum/10;
ListNode node =new ListNode(sum%10);
dummy.next=node;
l1=l1.next;
l2=l2.next;
dummy=dummy.next;
}
while(l1!=null){
int sum =l1.val+carry;
carry =sum/10;
ListNode node =new ListNode(sum%10);
dummy.next=node;
l1=l1.next;
dummy=dummy.next;
}
while(l2!=null){
int sum =l2.val+carry;
carry =sum/10;
ListNode node =new ListNode(sum%10);
dummy.next=node;
l2=l2.next;
dummy=dummy.next;
}
if(carry>0){
dummy.next=new ListNode(carry);
}
return pre.next;
}
}
- 看清题意,有时候需要做链表的反转。
19. 删除链表的倒数第 N 个结点
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
// 方式1: 遍历一遍,统计元素个数总和 ,再遍历
// 方式2: 快慢指针
// 定义一个哑结点,使得链表中所有的结点都有前驱结点
ListNode dummy = new ListNode(0,head);
// 定义快慢指针都指向哑结点
ListNode fast=dummy, slow=dummy;
// 让快指针先往前移动 n+1 步
for(int i=0;i<n+1;i++){
fast=fast.next;
}
// 同时移动快慢指针,直到快指针指向null
while(fast!=null){
fast=fast.next;
slow=slow.next;
}
// 不清理要删除元素所占的空间。
// slow.next=slow.next.next;
// 清理待删除元素所占的空间
ListNode delNode =slow.next;
slow.next=delNode.next;
delNode.next=null;
return dummy.next;
}
}
寻找链表的中间结点:
// 快慢指针,慢指针一次走一步,快指针一次走两步。最终慢指针指向就为中间结点
private ListNode endOfFirstHalf(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while (fast.next != null && fast.next.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
141. 环形链表
public class Solution {
public boolean hasCycle(ListNode head) {
Set<ListNode> seen = new HashSet<ListNode>();
while (head != null) {
if (!seen.add(head)) {
return true;
}
head = head.next;
}
return false;
}
}
面试题 02.06. 回文链表
- 其中包括获取中间结点的方法
- 链表反转的方法。
- 最终达到
class Solution {
public boolean isPalindrome(ListNode head) {
// 方式3:反转后半段链表,然后比较前后半段链表的值
// 1、通过快慢指针,找出链表的中间结点,慢指针的next结点为后半部分的开始
ListNode firstTail = getFirstHalf(head);
if(firstTail==null) return true ;
//2、反转后半部分链表
ListNode nextHalf= reversal(firstTail.next);
//3、比较将原链表和后半部分值比较。(不同return false, 相同返回true)
while(nextHalf!=null){
if(head.val!=nextHalf.val){
return false;
} else{
head=head.next;
nextHalf=nextHalf.next;
}
}
return true;
}
// 获取链表中间结点的方法
private ListNode getFirstHalf(ListNode head){
ListNode fast =head,slow =head;
while(fast!=null&&fast.next!=null&& fast.next.next!=null){
fast =fast.next.next;
slow=slow.next;
}
return slow;
}
// 链表反转
private ListNode reversal(ListNode node){
ListNode pre = null, cur=node,tem=null;
while(cur!=null){
tem =cur.next;
cur.next=pre;
pre=cur;
cur=tem;
}
return pre;
}
}
三、字符串:
- 字符串问题一般转换成char数组,去操作数组,省的每次操作字符串的
str.charAt(i)
1、验证子串是否为回文串
// char[] charArr =str.toCharArray();// 字符串转换成char数组
private static boolean validateSubstring(char[] charArr, int left ,int right){
while(left<right){
if(charArr[left]!=charArr[right]){
return false;
}
left++;
right--;
}
return true;
}
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd" 输出:"bb" 示例 3:
输入:s = "a" 输出:"a" 示例 4:
输入:s = "ac" 输出:"a"
提示:
1 <= s.length <= 1000 s 仅由数字和英文字母(大写和/或小写)组成
class Solution {
public String longestPalindrome(String s) {
// 特判
if(null==s || s.length()<2) return s;
// 中心扩散法
int res =1; //最大长度
int ll=0; //最大回文串的左指针
int rr=0; //最大回文串的右指针
//将字符串转成char数组,不在循环中去使用str.charAt(i)
char[] chArr =s.toCharArray();
// 开始遍历char数组
for(int i =0; i<chArr.length; i++){
// 以i为中心向两边扩散,寻找最长子串(通俗:回文串为奇数长度i为中心)
int l =i-1;
int r =i+1;
while(l>=0 && r<chArr.length && chArr[l]==chArr[r]){
int len =r-l+1;
if(len>res){
res=len;
ll=l;
rr=r;
}
l--;
r++;
}
// 以i为左指针,i+1为右指针(通俗:回文串为偶数长度)
l=i;
r=i+1;
while(l>=0 && r<chArr.length && chArr[l]==chArr[r]){
int len =r-l+1;
if(len>res){
res=len;
ll=l;
rr=r;
}
l--;
r++;
}
}
return s.substring(ll,rr+1);
}
}
58. 最后一个单词的长度
给你一个字符串 s,由若干单词组成,单词之间用空格隔开。返回字符串中最后一个单词的长度。如果不存在最后一个单词,请返回 0 。
单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
示例 1:
输入:s = "Hello World" 输出:5 示例 2:
输入:s = " " 输出:0
class Solution {
public int lengthOfLastWord(String s) {
/*//base case
if(null==s||s.equals(" ")) return 0;
String[] strArr=s.split(" ");
return strArr[strArr.length-1].length();*/
// 以上解法没有解决掉空格的问题
if(null==s||s.equals(" ")) return 0;
int end =s.length()-1;
//将结尾的空格去掉
while(end>=0 && s.charAt(end) == ' ') end--;
if(end<0) return 0;
//定义双指针,让其中一个指针移动,出现空格时结束,指针之差就是最后一个字符单词的长度。
int start = end;
while(start >=0 && s.charAt(start)!=' ')
start--;
return end-start;
}
}
392. 判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,
"ace"是"abcde"的一个子序列,而"aec"不是)。进阶:
如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
示例 1:
输入:s = "abc", t = "ahbgdc" 输出:true示例 2:
输入:s = "axc", t = "ahbgdc" 输出:false
class Solution {
public boolean isSubsequence(String s, String t) {
//方式1:双指针 ,定义两个指针,均指向s 和 t 的初始,然后对其值进行匹配 ,匹配成功,两指针均向右移动;匹配不成功只移动t的指针,
int i=0,j=0;
int sLen=s.length(), tLen =t.length();
while(i < sLen && j < tLen){
if(s.charAt(i)==t.charAt(j)){
i++;
}
j++;
}
return i == sLen;
}
}
四、树:
技巧:
- 递归最简单,一般树的问题都可以通过递归来解决。(需要再学下迭代,迭代是显示维护一个栈)
- 前序遍历:根左右;
中序遍历:左根右;后序遍历:左右根。
94. 二叉树的中序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
// 中序遍历:左 根 右
List<Integer> list = new ArrayList<Integer>();
leftOrder(root,list);
return list;
}
private void leftOrder(TreeNode node, List list){
if(null==node) return;
leftOrder(node.left,list);
list.add(node.val);
leftOrder(node.right,list);
}
}
剑指 Offer 32 - I. 从上到下打印二叉树
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
例如: 给定二叉树: [3,9,20,null,null,15,7],
3 / \ 9 20 / \ 15 7 返回:
[3,9,20,15,7]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int[] levelOrder(TreeNode root) {
//分层打印,需要引入队列,利用队列的先入先出的特性
if(root==null)return new int[]{};
Queue<TreeNode> queue =new LinkedList<>();
ArrayList<Integer> list =new ArrayList<>();
//先把根节点放入到队列中,
queue.add(root);
//如果队列不为空就一直遍历
while(!queue.isEmpty()){
//取出(移除)队列的第一个元素
TreeNode node =queue.remove();
//将当前节点元素值放入到List中
list.add(node.val);
//如果left不为空,放入到队列中
if(node.left!=null)
queue.add(node.left);
//如果right不为空,放入到队列中
if(node.right!=null)
queue.add(node.right);
}
int[] arr =new int[list.size()];
for(int i=0;i<list.size();i++){
arr[i]=list.get(i);
}
return arr;
}
}
五、栈:
六、Hash表
七、图
八、动态规划(labuladong)
动态规划的特点:
- 重叠子问题
- 状态转义方程(最关键)
- 最优子结构
题型:
- 求最值
- 核心:穷举:不要小看暴力穷举
解题套路:
- 明确【状态】
- 明确【选择】
- 明确dp函数、数组的定义
- 明确base case。



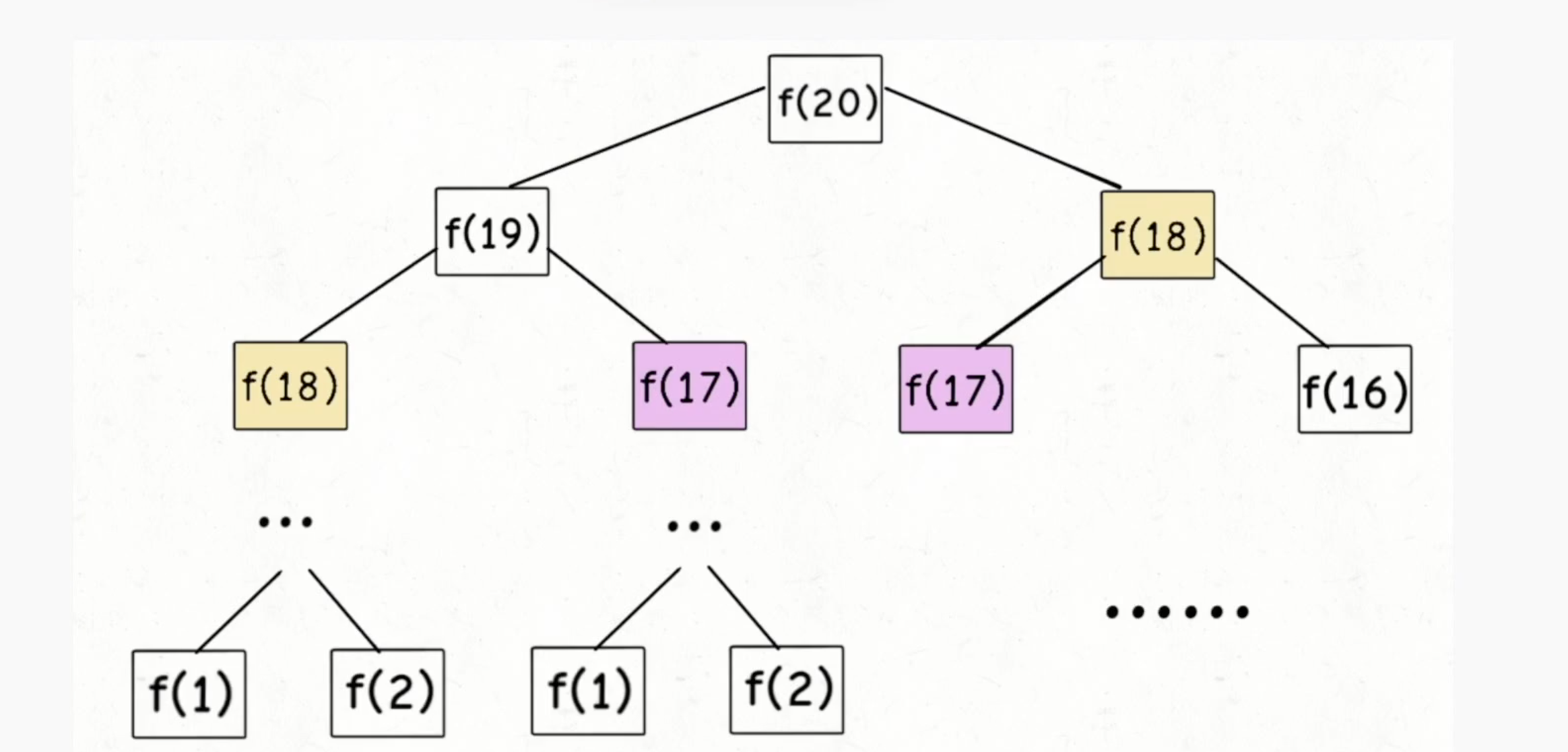
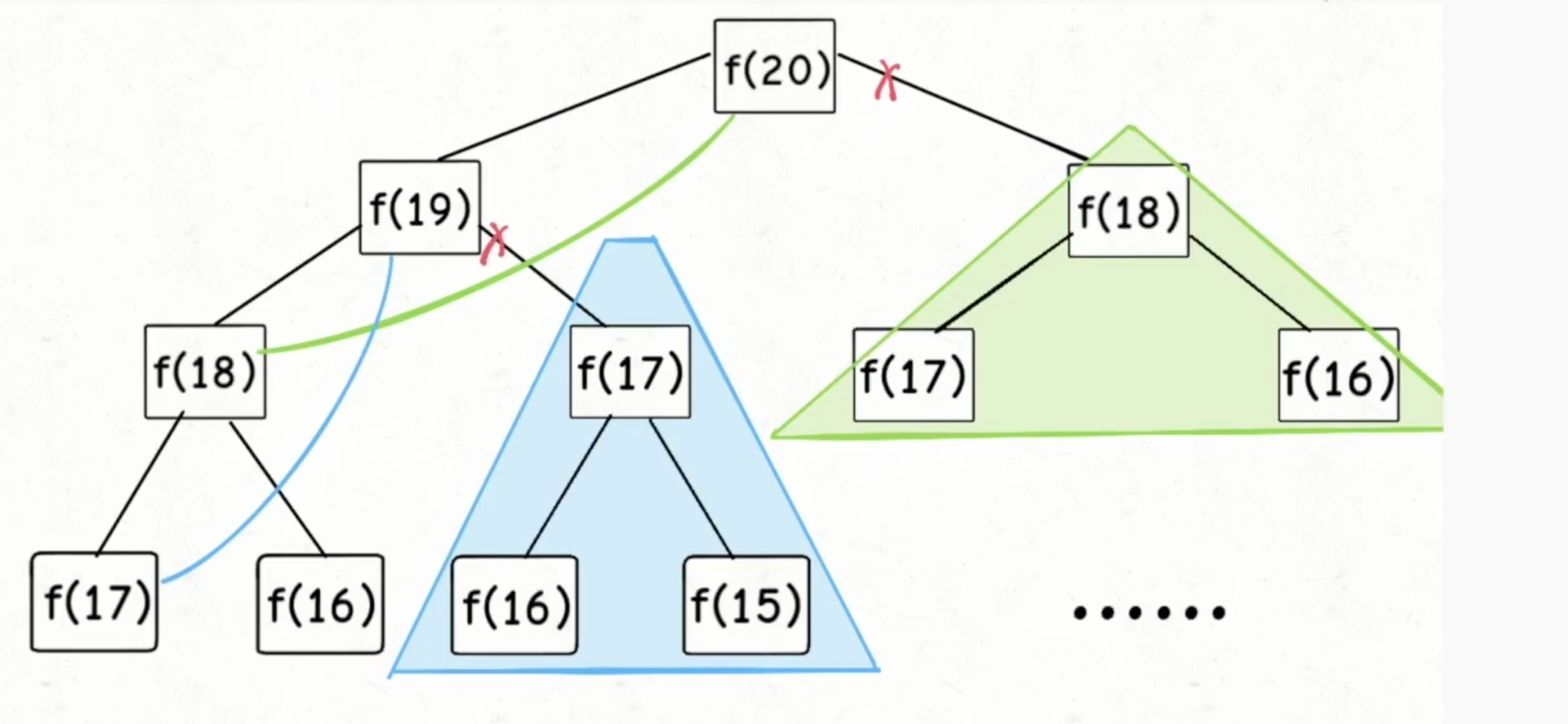
- 空间换时间。引入数组备忘录,占用数组大小的空间。
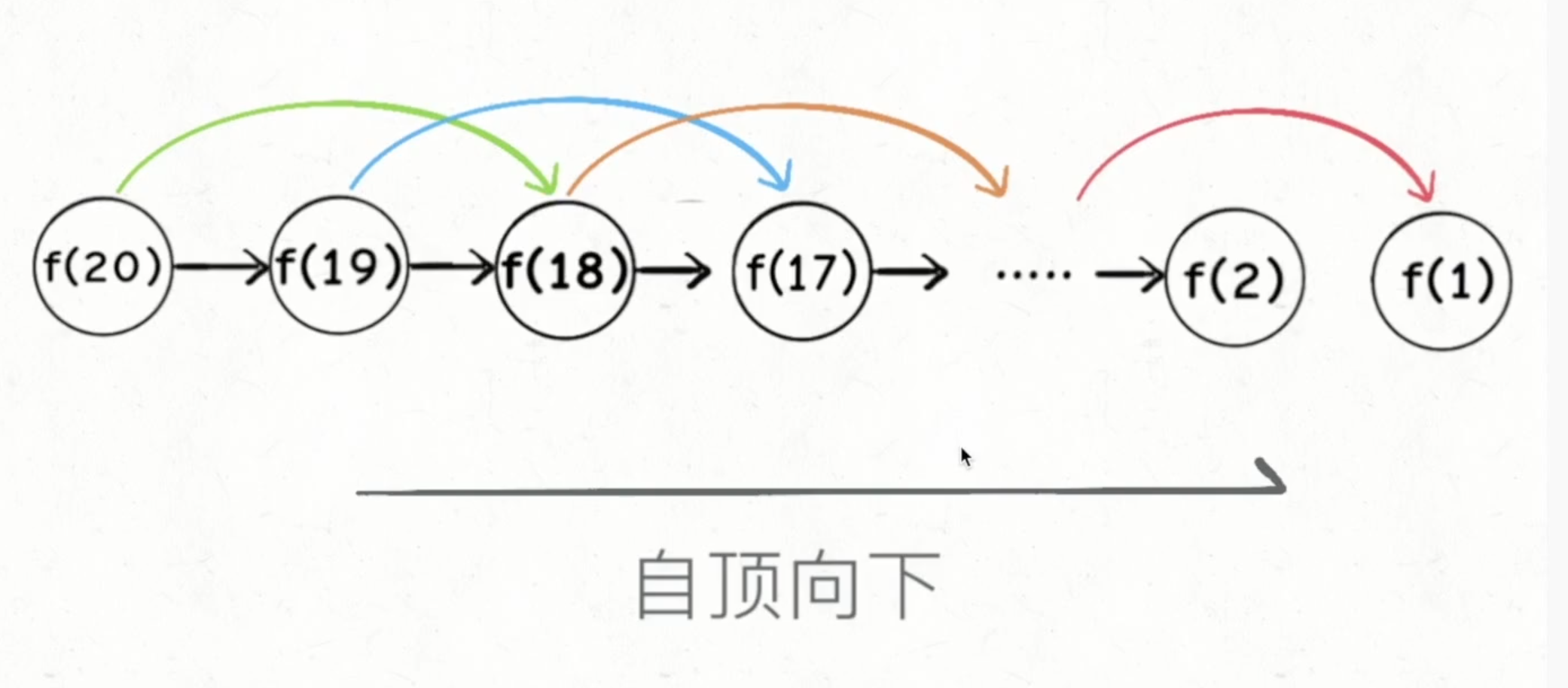
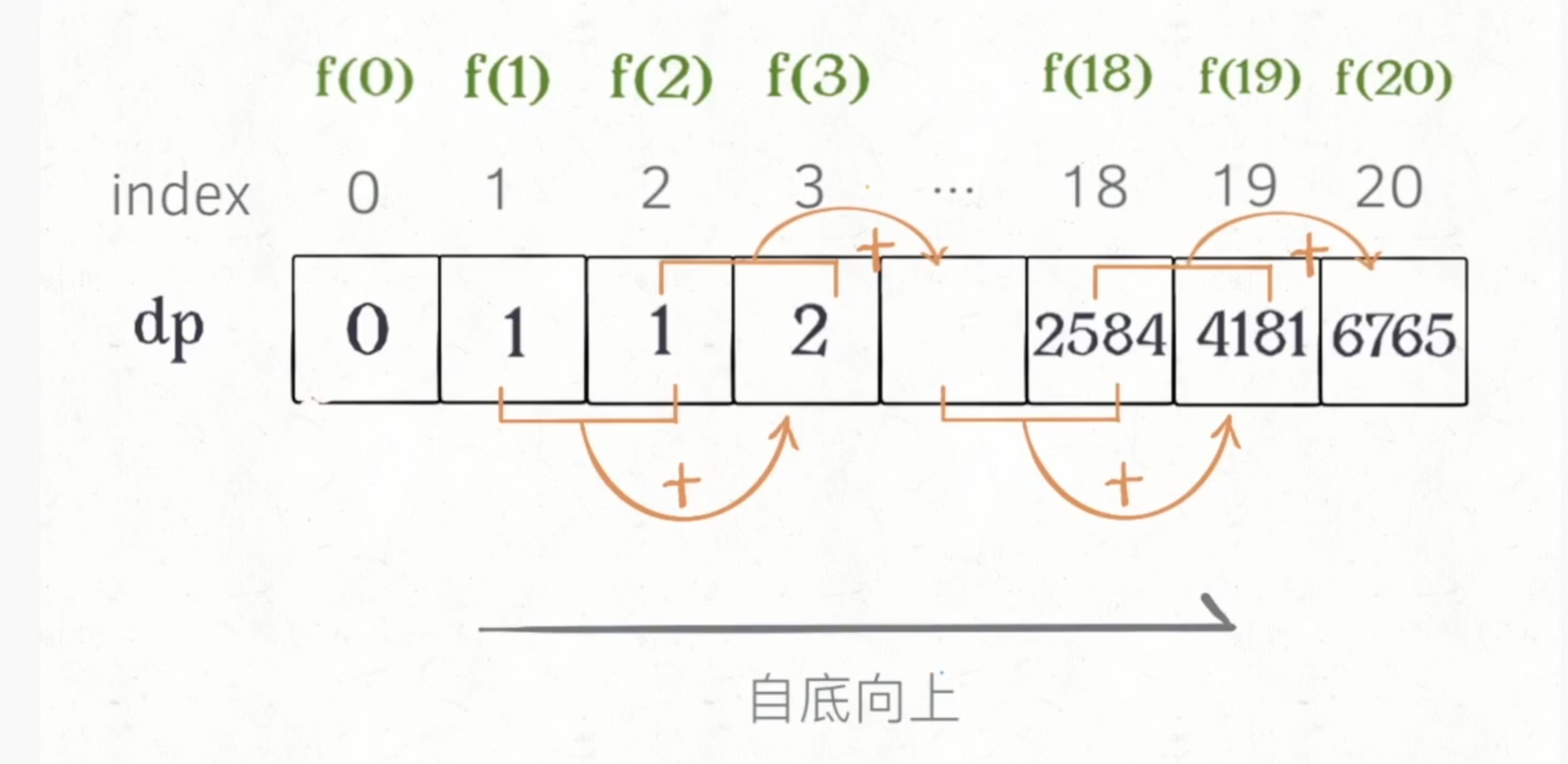
- 自底向上:
- 优秀的算法都是慢慢演变来的 ,就像系统架构一样,不是一开始就很优,都是慢慢演变的
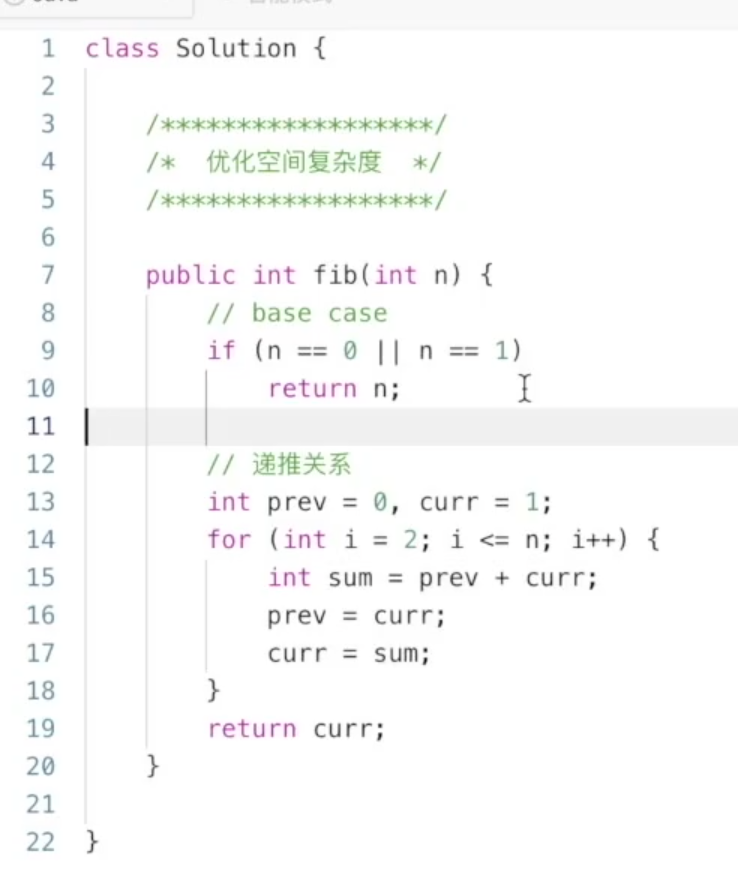
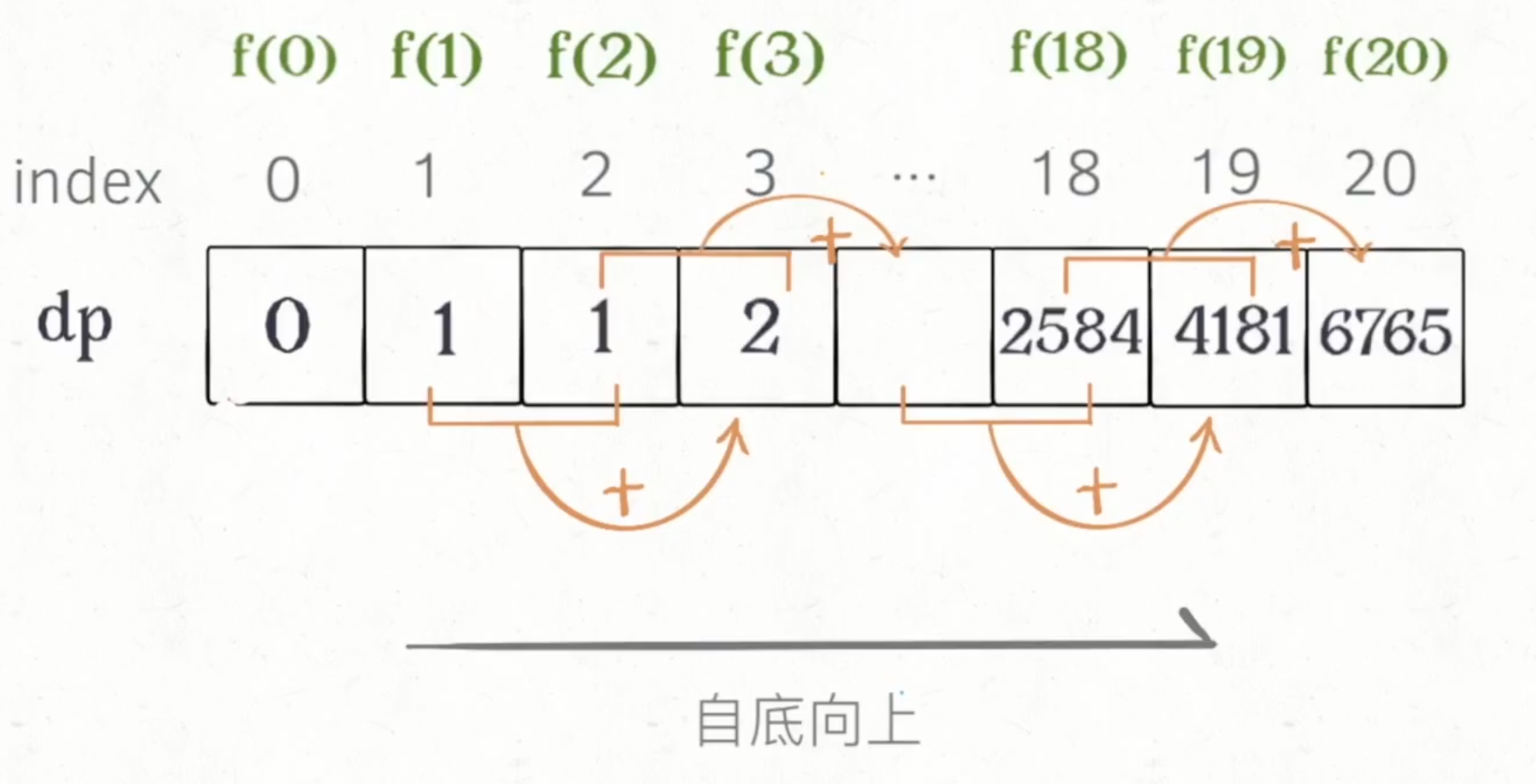
509:斐波那契数列
class Solution {
public int fib(int n) {
// 方式1:直接递归 ,但是时间复杂度较高,多了很多重复的计算。
/*// 方式2:带备忘录的递归。将所有计算过的值缓存下来,递归中直接返回。(自顶向下推,然后自底向上回溯)
// 初始化备忘录。
int[] notes =new int[n+1];
// 进行带备忘录的递归。
return helper(notes, n);*/
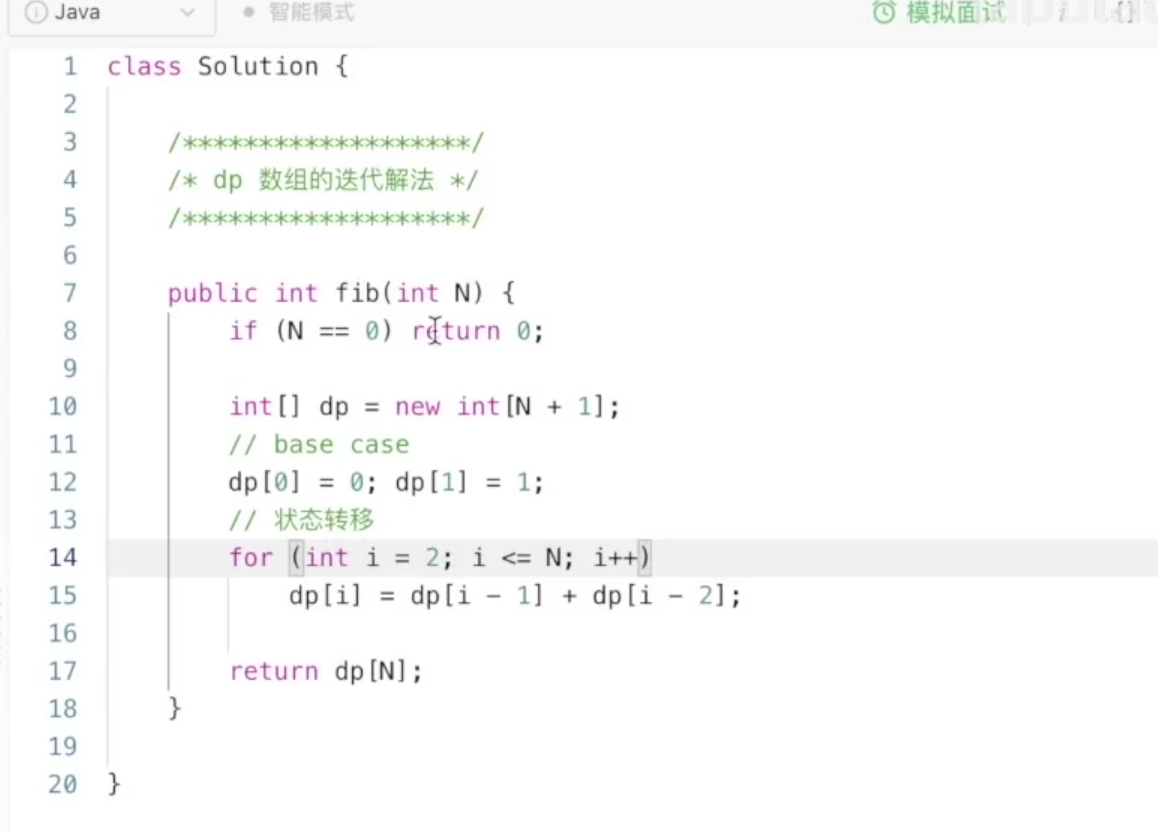
/* // 方式3:dp数组迭代法 (自底向上)
if(n==0) return 0;
int[] dp =new int[n+1];
// base case
dp[0]=0; dp[1]=1;
// 状态转移
for(int i=2; i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];*/
//方式4: 优化空间复杂度,求第n个数,其实只需要知道他的前两个数就可以了 ,
// 因此可以定义两个变量去表示它的前两个数的值,依次来优化空间复杂度
if(n==0) return 0;
int pre=0,curr=1;
for(int i=2;i<=n;i++){
int sum=pre+curr;
pre =curr;
curr=sum;
}
return curr;
}
private int helper(int[] notes,int n){
if(n==0|| n==1) return n; //base case
if(notes[n]!=0) return notes[n];
notes[n] =helper(notes,n-1)+helper(notes,n-2);
return notes[n];
}
}
322. 零钱兑换
- 动态规划 是用于求最值的问题。
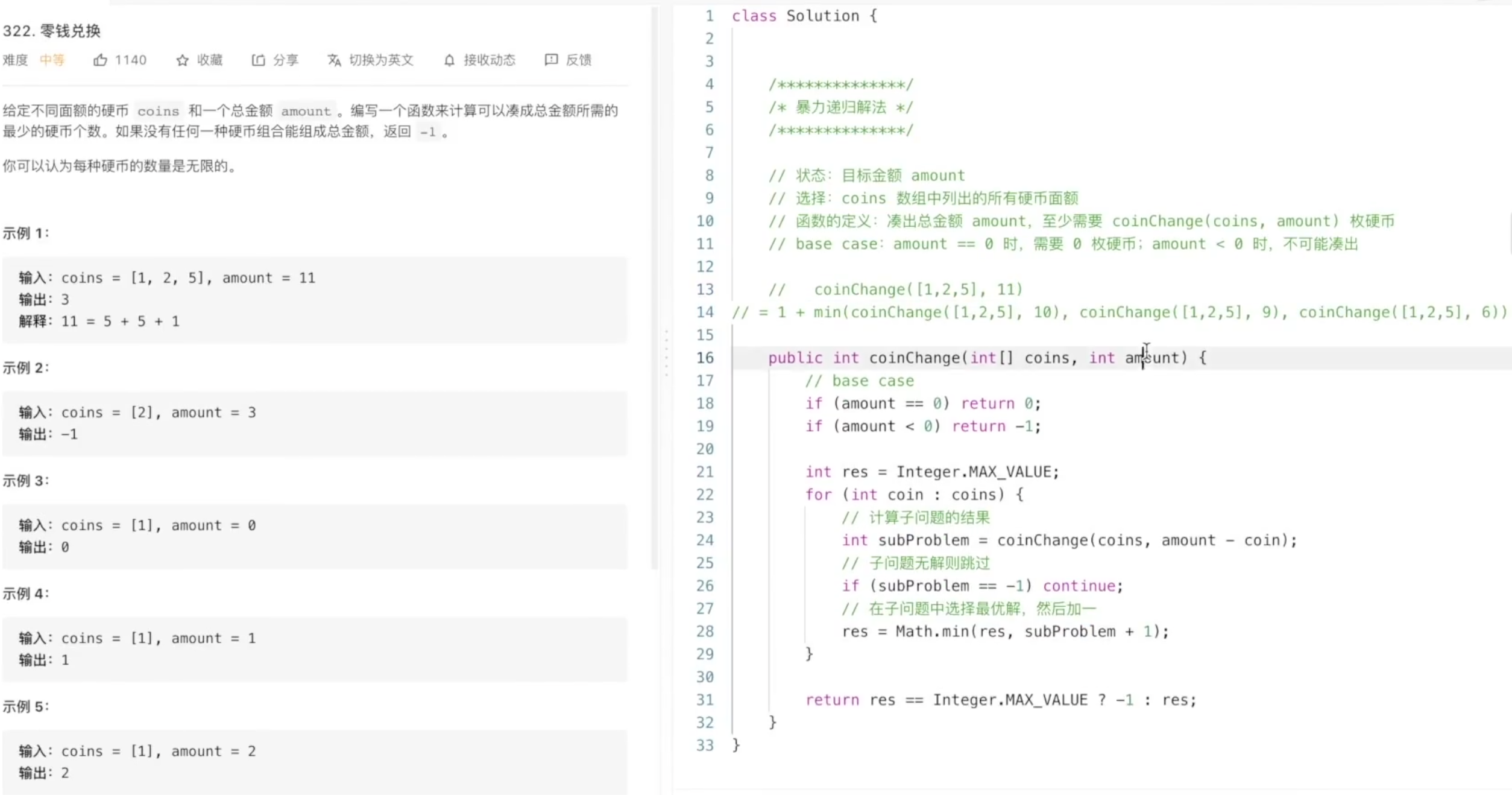
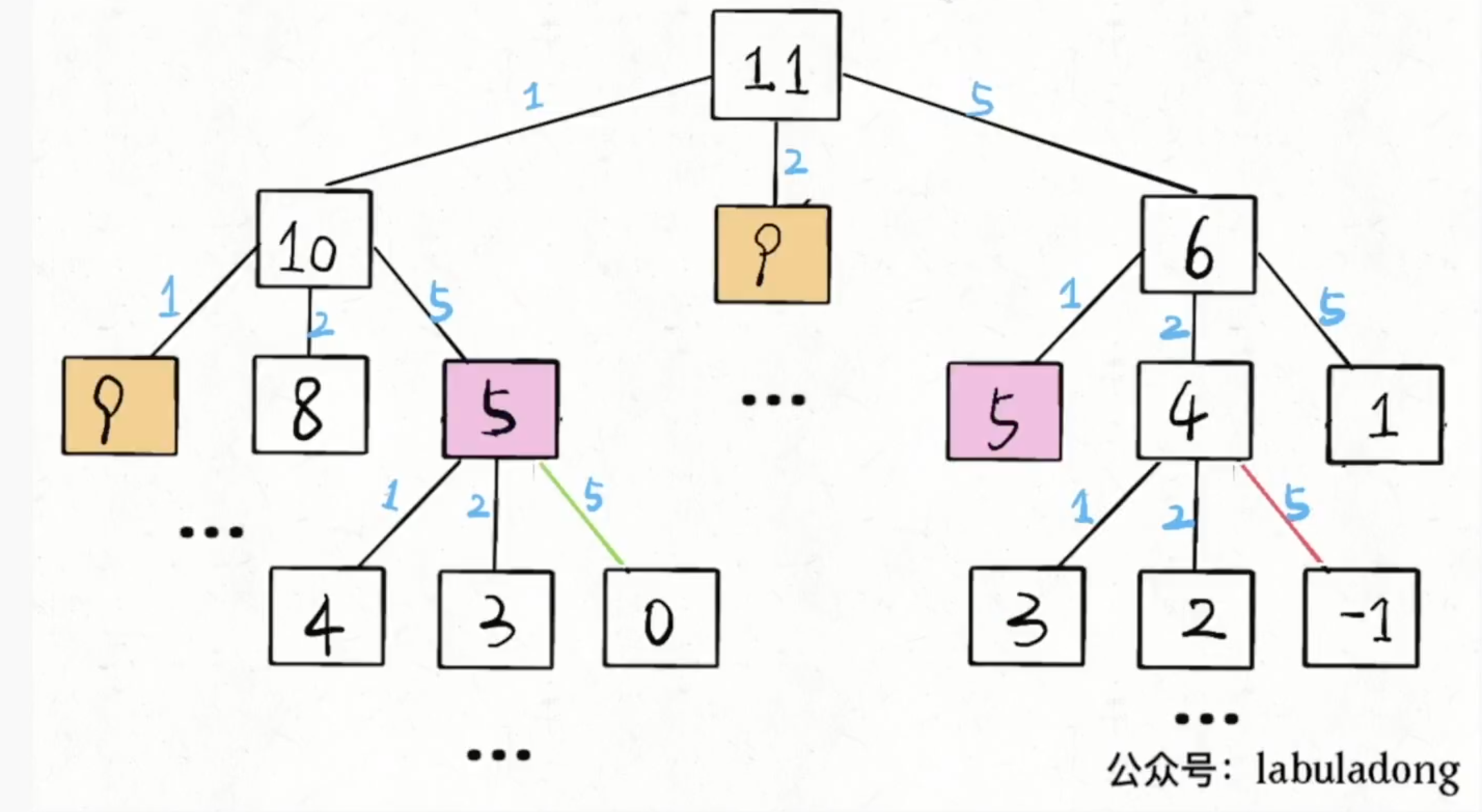
- 自顶向下的递归(带备忘录)
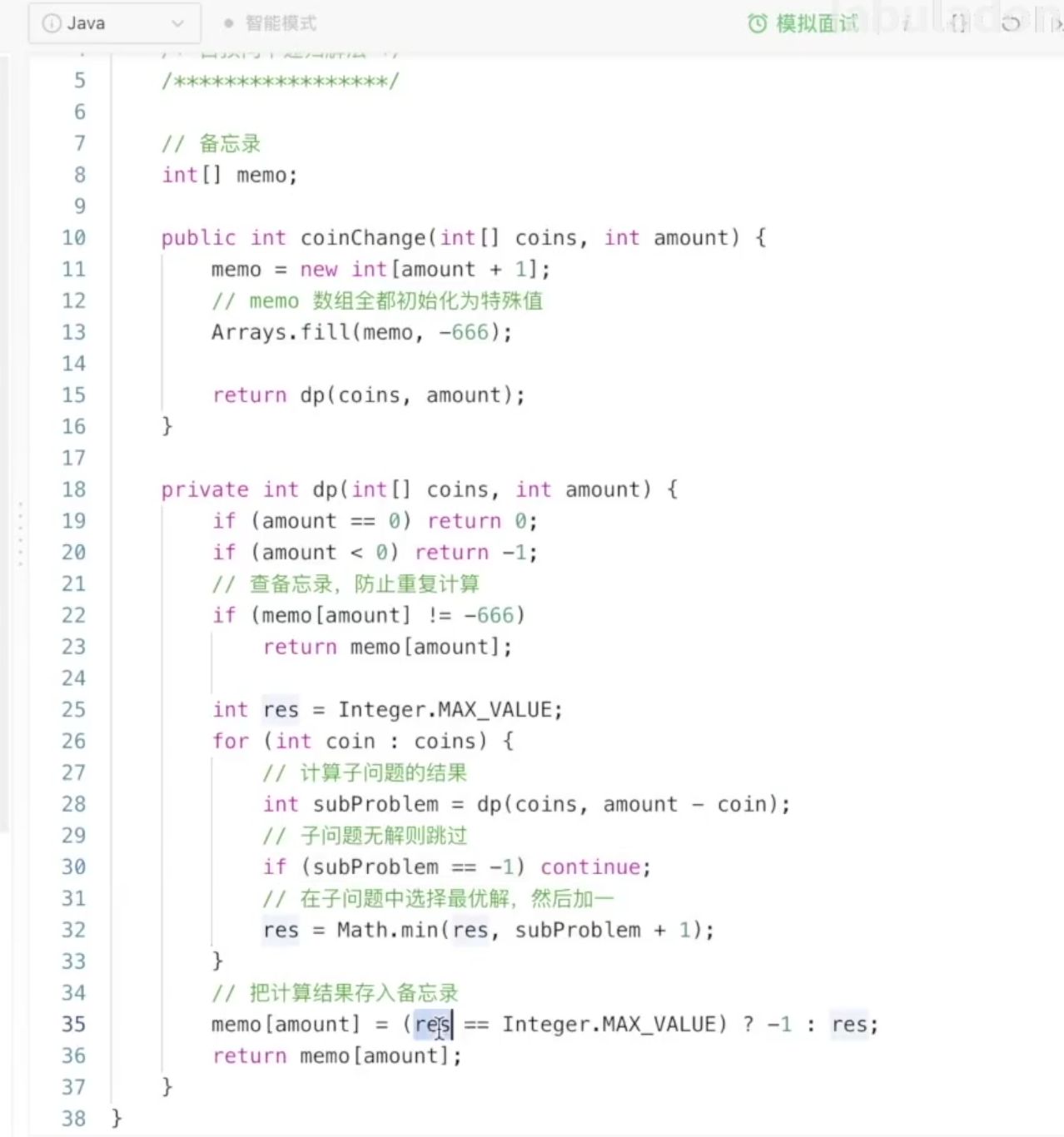
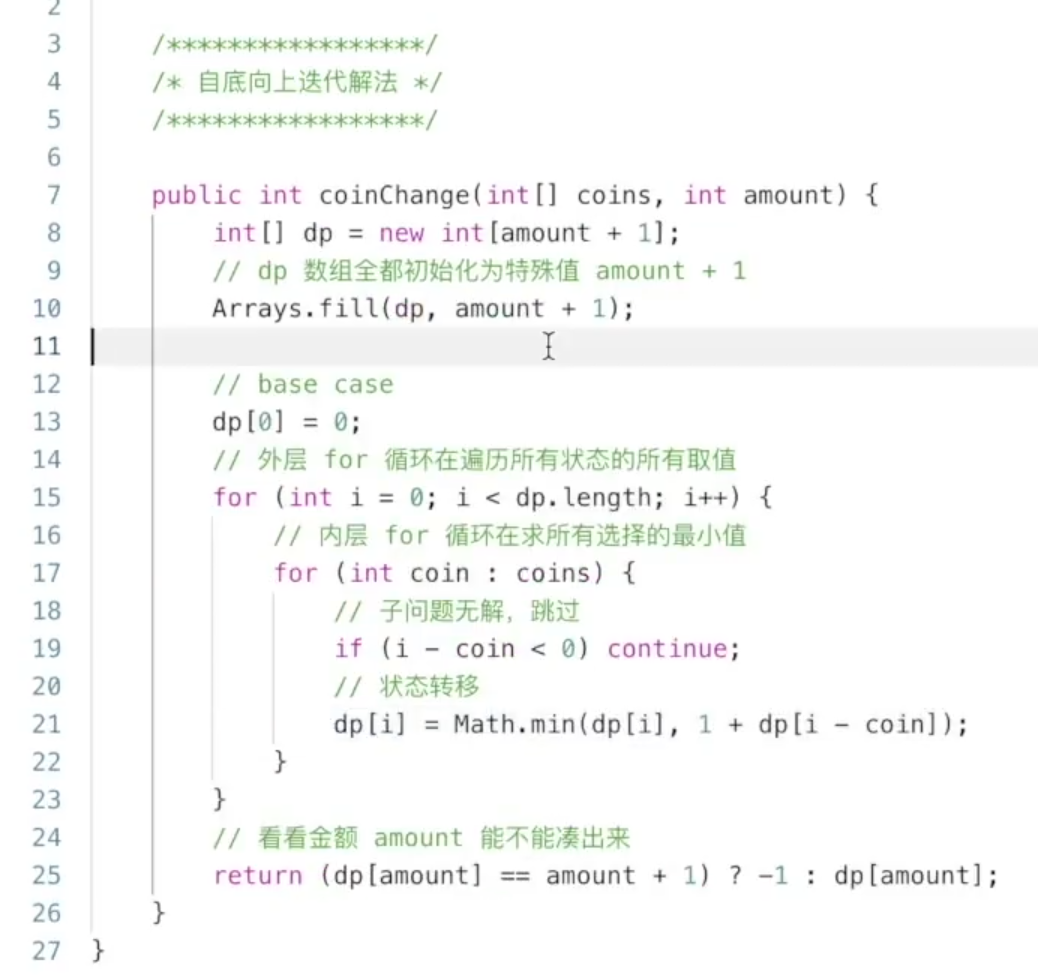
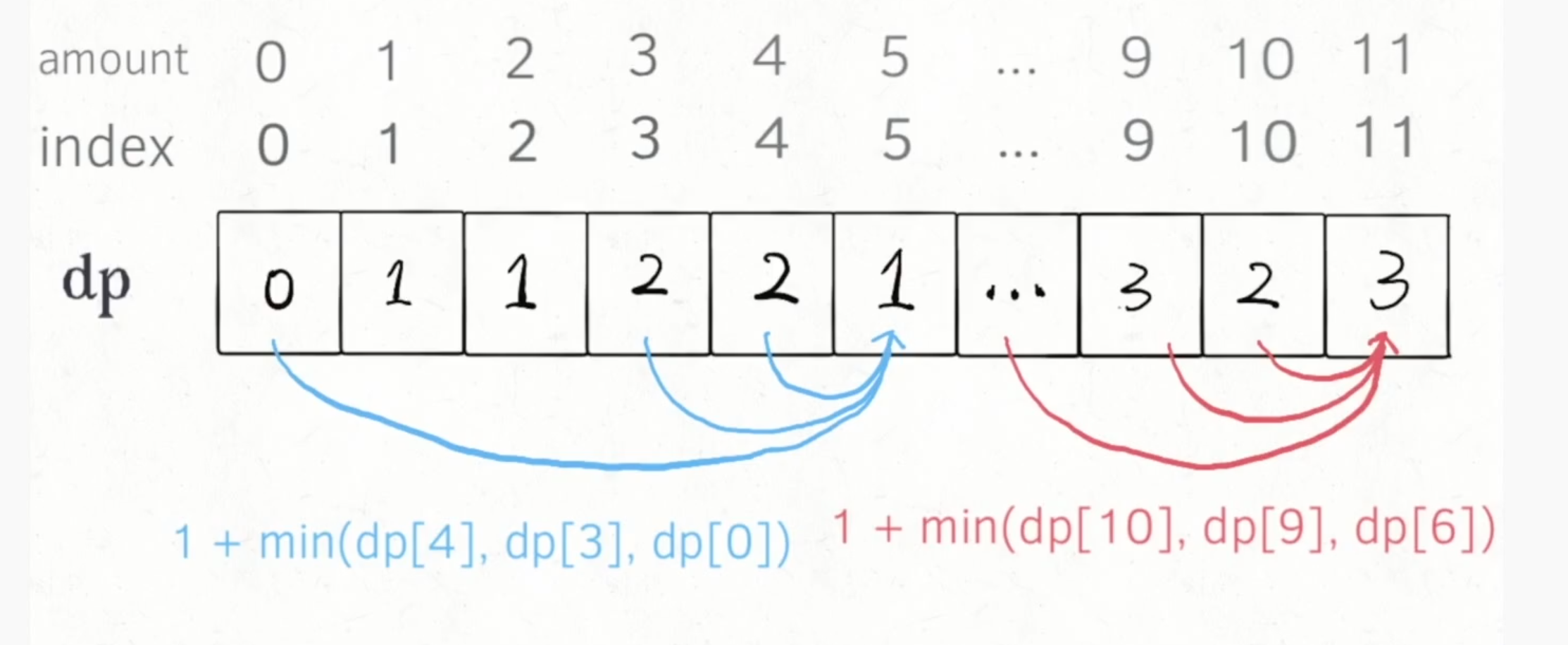
动态规划问题的本质:
- 1、如何穷举
- 写出状态转移方程,暴力穷举所有可行解。
- 2、如何聪明的穷举
- 用备忘录消除重叠子问题,写出自动向下解法
- 进一步,可以写出自动向下解法
- 再进一步,可能可以优化空间复杂度